正規分布（多変量）

リスク管理の要正規分布（多変量）

ポートフォリオ

大金持ちのあなたは、有り余る資産をどうしたものかと日々悩んでいます。あれこれ考えて土地、国内企業の株、海外企業の株、日本国債、金、ドル、ユーロ...様々な形で資産を保有することにしました。
それぞれの資産の価値は日々、否、時々刻々と変動しています。それぞれの資産の価値の変動は**正規分布（単変量）に従うとみなされます。気になるのは資産全体の価値の変動です。はたしてどのような変動に従うのでしょうか？
それぞれの資産価値がてんで勝手に変動するならば答えは簡単ですが、例えばドルが安くなると国内の株価が下がるなど、これらの資産はお互いに関連しあいながら変動することが分かっています。 つまり、各資産の変動を表す正規分布の情報（平均と標準偏差）に加えて、お互いにどのように関連しているかを表す情報が必要になります。それが相関**です。

相関係数

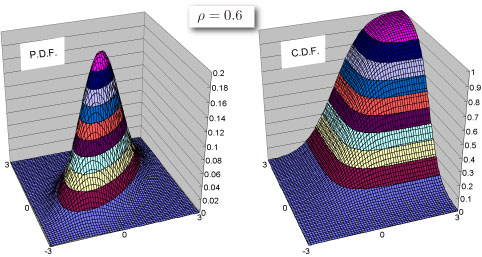
2変量の場合を考えてみましょう。標準正規分布に従っている2つの乱数 $z_1,;z_2$ を用意します。相関は相関係数 $\rho$（ギリシャ文字で "ロー"）と表記される場合が多く、

$$-1\leq \rho\leq 1$$

という範囲の値を取ります。$\rho$ の値によって

• $\rho = 0$：無相関
• $\rho > 0$：正の相関
• $\rho < 0$：負の相関

と分類されます。また$\rho =\pm 1$ の場合を完全相関といいます。\

相関行列

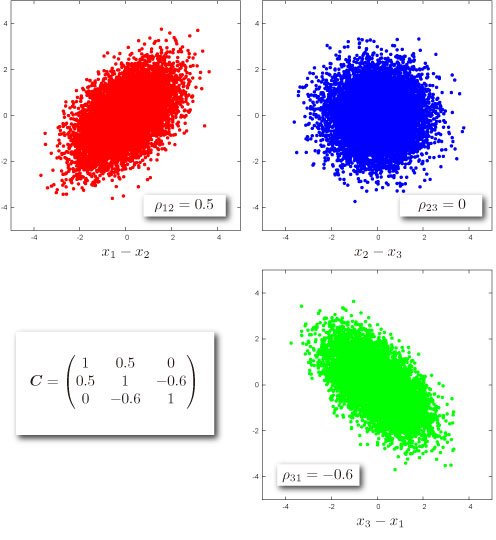
変数の数が3つになると、相関係数は変数の全てのペアで定義されます。変数1と変数2の相関係数を$\rho_{12}$のように書きます。$\rho_{12}=\rho_{21}$ であることに注意すれば、 結局$\rho_{12}$、$\rho_{13}$、$\rho_{23}$ の3つが必要となります。
さらに拡張して $n$ 個の変数がある場合は、

$$\begin{pmatrix}1&\rho_{12}&\rho_{13}&\cdots&\rho_{1n}\\rho_{12}&1&\rho_{23}&\cdots&\rho_{2n}\\vdots&\vdots&\vdots&\ddots&\vdots\\rho_{1n}&\rho_{2n}&\rho_{3n}&\cdots&1\end{pmatrix}$$

のように各相関係数を並べた相関行列によって変数間の相関が記述されます。

分布の形状

基本情報

• 変数の数が $n$ の場合、各変数の平均（$n$ 次元ベクトル）、各変数の標準偏差（$n$ 次元ベクトル $\mu$）、および各変数間の相関係数（$n\times n$ 行列。相関行列と呼ばれる）が必要です(実際には、標準偏差ベクトルと相関行列から求められる分散共分散行列 $\Sigma$ が計算に用いられます）。
• $n$ 次元のユークリッド空間 $R^{n}$ で定義される連続分布。

確率

• 確率密度関数

  $$f(x)=\frac{1}{(2\pi)^{n/2}\left|{\boldsymbol \Sigma}\right|^{1/2}}\exp\left[-\frac{1}{2}({\boldsymbol x}-{\boldsymbol \mu})^\prime{\boldsymbol \Sigma}^{-1}({\boldsymbol x}-{\boldsymbol \mu})\right]$$

• Excel での累積分布関数 (c.d.f.) と 確率密度関数 (p.d.f.)の求め方

	A	B
1	データ	説明
2	1.5	第1変数の対象となる値
3	-1	第2変数の対象となる値
4	1.5	第1変数の平均 M1
5	-1.2	第2変数の平均 M2
6	2	第1変数の標準偏差 Sigma1
7	0.7	第2変数の標準偏差 Sigma2
8	0.5	相関係数 Rho
9	数式	説明（計算結果）
10	=NTBINORMDIST((A2-A4)/A6,(A3-A5)/A7,A8,TRUE)	上のデータに対する累積分布関数の値
11	=NTBINORMDIST((A2-A4)/A6,(A3-A5)/A7,A8,FALSE)	上のデータに対する確率密度関数の値

• 関連 NtRand 関数 : NTBINORMDIST
• 第4引数がTRUEの場合のNTBINORMDISTNTBINROMDISTは、相関係数が $\rho=\pm 1$ かつ $x1=x2$ の場合にエラーとなります。

乱数

Excel での乱数生成法

	A	B	C	D
1	データ	データ	データ	説明
2	1.44	0.48	-0.36	cov. matrix
3	0.48	0.64	0	cov. matrix
4	-0.36	0	0.25	cov. matrix
5	データ	データ	データ	説明
6	1	2	3	mean vector
7	数式			説明 (計算結果)
8	=NTRANDMULTINORM(100,A2:C4,A6:C6)			(100×3）個の正規乱数を Mersenne Twister アルゴリズムで生成します。

メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A8:B1074 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

関連 NtRand 関数

• Mersenne Twiseter 法による乱数生成 : NTRANDMULTINORM
• 2変数正規分布の分布関数 : NTBINORMDIST

参照

• Wolfram Mathworld -- Multivariate Normal Distribution
• Wikipedia -- Multivariate normal distribution