Skip to main content

Normal Distribution (Multi Variable)

Where do you meet this distribution?​

  • Finance, Economics : Value at Risk

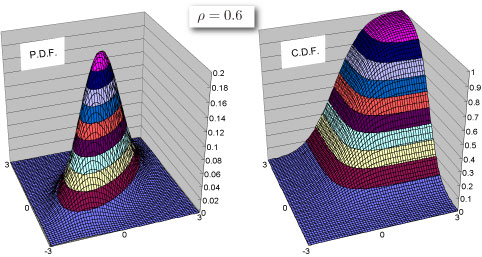
Shape of Distribution​

Basic Properties​

  • For n-variables, means for each variable (n-dimensional vector), standard deviations for each variable (n-dimensional vector μ\mu) and correlation coefficients for every pair of variables (n times n matrix. Called correlation matrix) are required (In practice, a covariance matrix Σ\Sigma calculated from standard deviation vector and correlation correlation matrix is required).
  • Continuous distribution defined on x∈Rnx\in R^{n}

Probability​

  • NTBINROMDIST is singular, when correlation coefficient ρ=±1\rho=\pm 1 and x1=x2.

  • Probability density function

    f(x)=1(2π)n/2∣Σ∣1/2exp⁡[−12(x−μ)′Σ−1(x−μ)]f(x)=\frac{1}{(2\pi)^{n/2}\left|\Sigma\right|^{1/2}}\exp\left[-\frac{1}{2}(x-\mu)^\prime\Sigma^{-1}(x-\mu)\right]

  • How to compute these on Excel.

AB
1DataDescription
21.5Value of 1st. variable for which you want the distribution
3-1Value of 2nd. variable for which you want the distribution
41.5Mean of variable1 M1
5-1.2Mean of variabel2 M2
62Standard deviation of variable1 Sigma1
70.7Standard deviation of variabel2 Sigma2
80.5Correlation coefficient Rho
9FormulaDescription (Result)
10=NTBINORMDIST((A2-A4)/A6,(A3-A5)/A7,A8,TRUE)Cumulative distribution function for the terms above
11=NTBINORMDIST((A2-A4)/A6,(A3-A5)/A7,A8,FALSE)Probability density function for the terms above

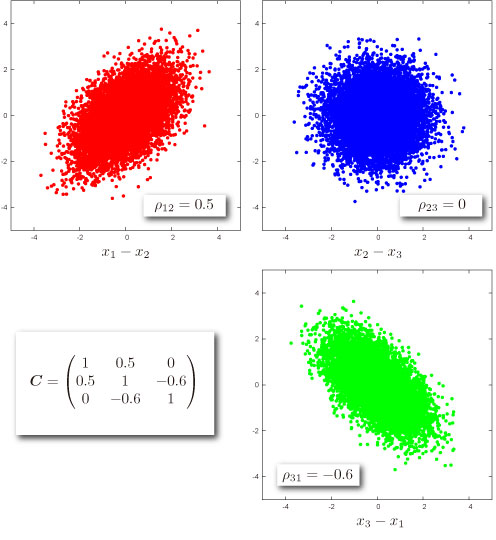
Random Numbers​

  • How to generate random numbers on Excel.
ABCD
1DataDataDataDescription
21.440.48-0.36cov. matrix
30.480.640cov. matrix
4-0.3600.25cov. matrix
5DataDataDataDescription
6123mean vector
7FormulaDescription (Result)
8=NTRANDMULTINORM(100,A2:C4,A6:C6)100 normal deviates (x 3 variables) for the terms above

NtRand Functions​

  • Generating random numbers based on Mersenne Twister algorithm: NTRANDMULTINORM
  • Computing probability for 2-variables : NTBINORMDIST

Reference​