// ホーム / 資料 / 分布関数の世界 / ベルヌーイ分布

ベルヌーイ分布(Bernoulli distribution)

来る？来ない？ベルヌーイ分布

「来る、来ない、来る、来ない…」
もう今ではやらないかもしれないけど、花びらをちぎって占った経験、小さい時にありませんでしたか？
ゲームの先攻・後攻を決めるコイントスだったり（日本ではジャンケンが主流ですが）、
はたまた持ってる株の値段が上がるか下がるか…ハラハラドキドキですね。

このように、2つの状態しか現れない事象をモデル化したのが「ベルヌーイ分布」と呼ばれるものです。
コイントスをイメージすると表が出るか裏が出るかは5分5分だと思うかもしれませんが、 コインは曲がっているかもしれないし、イカサマをしてコインの表側に重りが貼り付けてあるかもしれないですもんね。 つまり、確率は5分5分とは限らず、4:6かもしれないし、3:7かもしれないということなんです。
一般にベルヌーイ分布は、成功（あの子が来る、コインの表が出る（勿論賭けた方）、株価が上がる）を 1、失敗を 0 として、
  • 確率 p で1が出る（成功）
  • 確率 (1-p) で0が出る（失敗）
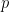と表現し、p のことを「成功確率」と呼びます。
p = 0.5 の場合は、成功と失敗の確率が同じとなって、この場合に限り、下限が0、上限が1の一様分布（離散）と同じになる。 つまり0か1の一様分布ですね。

ある営業マンの悲劇：ベルヌーイ試行を使って

ベルヌーイ分布はそれだけで使うことはあまりなく、ベルヌーイ分布に従う乱数を多数生成した場合→つまりコイントスを何度もして（1つ1つのコイントスをベルヌーイ試行といいます）その積み重ねの確率的性質を調べる時に用いられます。 単純な例では、コイントスを100回して表が何回出るかを調べる、といったものがあります。
もう少しストーリー性のあふれる例で見てみましょう。

僕は新人サラリーマン。研修を終え、配属されたのは営業部。 この夏は社運を賭けた新製品を大々的に売り出すことになった。僕ら新人も微力ながら販売に力を尽くすことを命じられた。新人は飛び込み営業が基本だ。 よーし、売って売って売りまくるぞ！！

さっそく担当地区に送りだされて、営業を始める。1件目。ドアも開けてくれない。2件目。勢いが空回りしてダメだった。3件目。ここもダメ…。午前中はあっという間に過ぎ、公園でさっき買ったマクドにかぶりつきながら先輩の言葉を思い出す。 「まぁ、50件回って2件でも買ってくれたら良い方じゃないか？」…そうか、すると売れる確率は p=2/50=0.04 ってところか。
じゃあ…？
  • 最初に買ってくれるお客さんにめぐり合うまで、何件のドアを叩かなければならないか？
  • 今日一日250件回って、何件の売り上げが期待できるか？
なんてことをぼんやり考えてみる。
最初の疑問には幾何分布を利用する。幾何分布の期待値はベルヌーイ試行の成功確率 p の逆数だ。…ってことは、1/p=1/0.04=25 これに1を加えた 26 件となる。絶望的というほどのことはないか。
次の疑問には二項分布が答えをくれる。二項分布の期待値はベルヌーイ試行の成功確率 p と試行回数、つまり訪問件数の積だ。ってことは、250件回れば 250\times p=250\times 0.04=10 件か。 50件に2件なら250件回れば10件。当然の結果か。

もう一例、別の日を見てみましょう。
今日もまた飛び込み営業だ。でも今日のエリアは裕福な人が多い。過去の実績からいって20件に1件は買ってもらえる。つまり、成功確率は p=1/20=0.05 ってことだ。
  • 今日のノルマは12件。では、結果何件回ることになるだろうか？
この答えはパスカル分布（別名負の二項分布）で明白になる。パスカル分布では指定した回数成功する（この場合12件）までの試行数の期待値は、ベルヌーイ試行の成功確率 p=0.05 を使って、12\times\frac{1-p}{p}=12\times\frac{1-0.05}{0.05}=228[件] となる。
やっぱり今日も長い一日になりそうだな。

その他のネタ

公正なコイン（成功確率 1/2）を使って表が出たら +1、裏が出たら -1 とした場合、ベルヌーイ分布によく似ていますが、この場合の分布にはラデマッハー分布という名前が付いています。

分布の形状

基本情報

  • 1つのパラメータ p\;(0< p< 1) が必要です。 このパラメータは成功確率と呼ばれます。
  • 整数 x=\{0, 1\} で定義された離散分布です。

確率

分布の特徴

平均 – 分布の”中心”はどこ？ (定義)

  • 分布の平均 は p と与えられます。

標準偏差 – 分布はどのくらい広がっているか（定義）

歪度 – 分布はどちらに偏っているか(定義)

  • 分布の歪度 は次式で与えれらます。
    \frac{1-2p}{\sqrt{p(1-p)}}

尖度 – 尖っているか丸まっているか (定義)

  • 分布の尖度 は次式で与えられます。
    \frac{6p^2-6p+1}{p(1-p)}

乱数

Excel での乱数生成法
 
1
2
3
4
   
AB
データ説明
0.3 分布のパラメータ p の値
数式説明（計算結果）
=IF(NTRAND(100)<A2,0,1) 100個のベルヌーイ乱数を Mersenne Twister アルゴリズムで生成します。

メモ： この使用例の数式は、配列数式として入力する必要があります。使用例を新規ワークシートにコピーした後、A4:A103 のセル範囲 (配列数式が入力されているセルが左上になる) を選択します。F2 キーを押し、Ctrl キーと Shift キーを押しながら Enter キーを押します。この数式が配列数式として入力されていない場合、単一の値 2 のみが計算結果として返されます。

参照

 

Comments are closed.