// Home / Documentation / Gallery of Distributions / Normal distribution (Multi variables)

Normal distribution (Multi variables)

Where do you meet this distribution?

  • Finance, Economics : Value at Risk

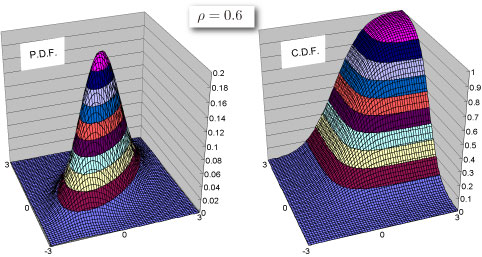
Shape of Distribution

Basic Properties

  • For n-variables, means for each variable (n-dimensional vector), standard deviations for each variable (n-dimensional vector \mu) and correlation coefficients for every pair of variables (n times n matrix. Called correlation matrix) are required (In practice, a covariance matrix \Sigma calculated from standard deviation vector and correlation correlation matrix is required).
  • Continuous distribution defined on x\in R^{n}

Probability

  • NTBINROMDIST is singular, when correlation coefficient \rho=\pm 1 and x1=x2.
  • Probability density function
    f(x)=\frac{1}{(2\pi)^{n/2}\left|\Sigma\right|^{1/2}}\exp\left[-\frac{1}{2}(x-\mu)^\prime\Sigma^{-1}(x-\mu)\right]

    • li>How to compute these on Excel.

     
    1
    2
       
    3
       
    4
    5
    6
    7
    8
    9
    10
       
    11
       
    A B
    Data Description
    1.5 Value of 1st. variable for which you want the distribution
    -1 Value of 2nd. variable for which you want the distribution
    1.5 Mean of variable1 M1
    -1.2 Mean of variabel2 M2
    2 Standard deviation of variable1 Sigma1
    0.7 Standard deviation of variabel2 Sigma2
    0.5 Correlation coefficient Rho
    Formula Description (Result)
    =NTBINORMDIST((A2-A4)/A6,(A3-A5)/A7,A8,TRUE) Cumulative distribution function for the terms above
    =NTBINORMDIST((A2-A4)/A6,(A3-A5)/A7,A8,FALSE) Probability density function for the terms above

  • Function reference : NTBINORMDIST

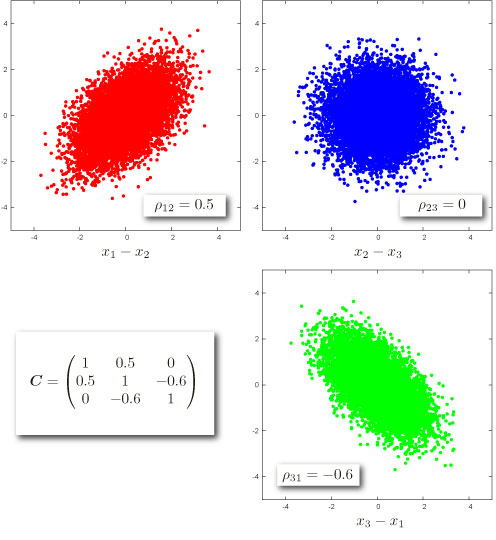
Random Numbers

  • How to generate random numbers on Excel.
     
    1
    2
    3
    4
    5
    6
    7
    8
       
    A B C D
    Data Data Data Description
    1.44 0.48 -0.36 cov. matrix
    0.48 0.64 0 cov. matrix
    -0.36 0 0.25 cov. matrix
    Data Data Data Description
    1 2 3 mean vector
    Formula     Description (Result)
    =NTRANDMULTINORM(100,A2:C4,A6:C6)     100 normal deviates (x 3 variables) for the terms above

NtRand Functions

Reference

 

Comments are closed.